| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- cnn
- Circuit
- dnf
- 십진법
- 모순명제
- truth table
- Contradiction
- 진리표
- Logical statement
- Digital Logic Circuits
- half adder
- Sentiment Analysis
- ermodel
- statement equivalence
- GPT-1
- relationaldatabaseschema
- full adder
- 써킷
- 모두의네트워크
- Gate
- 항진명제
- 모두의네트워크정리
- Decimal notation
- 모두의네트워크요약
- Tautology
- 이진법 십진법 변환
- Binary notation
- CNF
- 명제 동치
- 명제
- Today
- Total
목록Foundation of Computing (7)
NLP Learner in Switzerland
 Digital Logic Circuits Lab Exercise(DNF, CNF, Circuit, half adder, full adder)
Digital Logic Circuits Lab Exercise(DNF, CNF, Circuit, half adder, full adder)
Chapter : Digital Logic Circuits Topic : DNF, CNF, Circuit, half adder, full adder 1. 3개의 스위치가 ON인 경우를 주고 logical formula 및 circuit을 도출하라는 문제이다. 2. 2개 이상 켜지면 ON이므로 2개만 켜져있다면 나머지 1개의 상태는 1이든 0이든 상관이 없다. 따라서 a and b, b and c, a and c 세가지 경우가 있다. 이를 이용해서 s의 logical expression을 도출해내고, circuit을 그렸다. 3. Solution 아래 이미지 참조. 1. i. NANA( NOT AND) gate만 가지고 XOR(OR but not BOTH) gate를 만드는 문제이다. ii. XOR과 AN..
 Digital Logic Circuits Lab Exercise(DNF, CNF, Circuit)
Digital Logic Circuits Lab Exercise(DNF, CNF, Circuit)
Chapter : Digital Logic Circuits Topic : DNF, CNF, Circuit 1. 5개의 스위치가 ON인 경우를 주고 logical formula 및 circuit을 도출하라는 문제이다. 2. 2개 이상 켜지면 ON인데, 이건 경우의 수가 많다. 따라서 반대로 하나도 안 켜지거나 1개만 켜진 케이스를 나열했다. 그 후 CNF로 s의 logical expression을 도출해내고, circuit을 그렸다. 3. Solution 아래 이미지 참조. 1. NAND(NOT AND) gate로만 OR gate를 만들어내는 문제이다. 2. a OR b = a∨b의 logical expression을 확장시켜서 NOT AND = ~(a∧b)의 형태로 나타낼 수 있도록 만들어본다. 3. S..
 Digital Logic Circuits Lab Exercise(Binary/Decimal notation, DNF, CNF, Circuit)
Digital Logic Circuits Lab Exercise(Binary/Decimal notation, DNF, CNF, Circuit)
Chapter : Digital Logic Circuits Topic : Binary/Decimal notation, DNF, CNF, Circuit 1. 주어진 십진수를 이진수로 변환하는 문제이다. 2. 십진수-이진수 변환은 중딩때인가 나오는 매우 쉬운 내용이므로 그냥 풀면 된다... 2. Solution 아래 이미지 참조. 1. 주어진 이진수를 십진수로 변환하는 문제이다. 2. 2의 제곱,세제곱,네제곱을 해가면서 더하는 방법도 있긴 한데(중딩때 이 방법으로 배움), 수업시간에 배운 Doubling이라는 방법을 사용해서 풀었다. 이게 더 간단한 듯. 3. Solution 아래 이미지 참조. 1. 주어진 이진수 합계산을 수행하고 십진수로 변환하는 문제이다. 2. 십진수일 때처럼 동일하게 합계가 10을 넘..
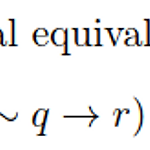 Propositional Logic Lab Exercise(logical statement, truth table)
Propositional Logic Lab Exercise(logical statement, truth table)
Chapter : Propositional Logic Topic : Logical statement, Truth table, Tautology, Contradiction, statement equivalence Solution : Equivalence가 성립한다. 1. 주어진 logical equivalence가 성립하는지 판단하는 문제이다. 2. p→(~q→r) ≡ ~p∨(~q→r) ≡ ~p∨(q∨r) 좌변과 일치한다. Solution : tautology 1. 주어진 statement가 tautology(t)인지 contradiction(c)인지 판단하는 문제이다. 2. (p∨q)∨~(p∨q) ≡p∨q∨~p∨~q ≡ tautology(t) Solution : tautology(t)과 contradic..
 Propositional Logic Exercise(logical statement, complicated statement simplifying)
Propositional Logic Exercise(logical statement, complicated statement simplifying)
Chapter : Propositional Logic Topic : Logical statement, complicated statement simplifying and equivalence Solution : tautology(t)가 성립한다. 1. 주어진 statemen를 simplifying했을 때 tautology가 성립하는지 판단하는 문제이다. 2. (a↔b)↔(a→b)∧(b→a) ≡ (a→b)∧(b→a)↔(a→b)∧(b→a) --- a↔b≡(a→b)∧(b→a) ≡ (~a∨b)∧(~b∨a)↔(~a∨b)∧(~b∨a) --- a→b≡(~a∨b)∧(~b∨a) ≡ (x∧y)↔(x∧y) --- x=(~a∨b) / y=(~b∨a) ≡ (x∧y→x∧y)∧(x∧y→x∧y) ≡ (x∧y→x∧y) --- p∧p≡..
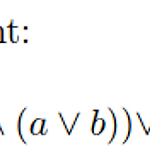 Propositional Logic Exercise(logical statement, statement simplifying)
Propositional Logic Exercise(logical statement, statement simplifying)
Chapter : Propositional Logic Topic : Logical statement, statement simplifying Solution : b∨~d 1. 주어진 statement를 simplifying하는 문제이다. 2. (~a∧(a∨b))∨~d∨(b∧d) ≡ [(~a∧a)∨(~a∧b)]∨[(~d∨b)∧(~d∨d)] --- 분배법칙 ≡ (~a∧b)∨(~d∨b) --- (~a∧a)=c / (~d∨d)=t ≡ ((~a∧b)∨b)∨~d --- 결합법칙으로 b랑 ~d의 자리를 바꿔준 것 ≡ ((~a∧b)∨(b∧t))∨~d --- 여기가 좀 까다로운데 흡수법칙을 사용했다. (흡수법칙 : p∨(p∧q)≡p) ≡ (b∧(~a∨t))∨~d --- 분배법칙 ≡ (b∧t)∨~d --- (~a∨t)=t..
 Propositional Logic Exercise(logical statement, truth table)
Propositional Logic Exercise(logical statement, truth table)
Chapter : Propositional Logic Topic : Logical statement, Truth table, Tautology, Contradiction, statement equivalence Solution : iii, vi 1. All dogs are loyal의 negation을 찾는 문제이다. 2. 단편적으로 생각해보면 All dogs are not loyal일 것 같지만 세상이 그렇게 만만하지 않다. 3. All dogs are loyal = (dog1 is loyal) and (dog2 is loyal) and (dog3 is loyal) and ... (dog(n) is loyal)으로 decompostion된다. 그리고 여기에 negation을 취하면 4. ~(All do..
