| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 모두의네트워크정리
- 명제 동치
- statement equivalence
- Tautology
- 모두의네트워크
- 모순명제
- 진리표
- 십진법
- CNF
- full adder
- Logical statement
- GPT-1
- Digital Logic Circuits
- 써킷
- 항진명제
- Gate
- 이진법 십진법 변환
- relationaldatabaseschema
- dnf
- truth table
- Circuit
- ermodel
- 명제
- Sentiment Analysis
- half adder
- cnn
- Decimal notation
- 모두의네트워크요약
- Binary notation
- Contradiction
- Today
- Total
NLP Learner in Switzerland
Propositional Logic Lab Exercise(logical statement, truth table) 본문
Propositional Logic Lab Exercise(logical statement, truth table)
초코빵 2021. 5. 18. 05:00
Chapter : Propositional Logic
Topic : Logical statement, Truth table, Tautology, Contradiction, statement equivalence

Solution : Equivalence가 성립한다.
1. 주어진 logical equivalence가 성립하는지 판단하는 문제이다.
2. p→(~q→r)
≡ ~p∨(~q→r)
≡ ~p∨(q∨r)
좌변과 일치한다.

Solution : tautology
1. 주어진 statement가 tautology(t)인지 contradiction(c)인지 판단하는 문제이다.
2. (p∨q)∨~(p∨q)
≡p∨q∨~p∨~q
≡ tautology(t)

Solution : tautology(t)과 contradiction(c) 모두 아니다.
1. 위 문제와 동일하게 주어진 statement가 tautology(t)인지 contradiction(c)인지 판단하는 문제이다.
2. ((p∧~q∧~r)∨(p∧~q∧r))↔~(p∨q)
좌변을 풀어보면
≡ (p∧~q)∧(~r∨r) --- 분배법칙
≡ (p∧~q) --- (~r∨r)=t
따라서 전체 statement를 다시 쓰면
≡ (p∧~q)↔~(p∨q)
이제 변수의 수가 적으므로 truth table이 더 간단할 수도 있다.(bicomditional statement는 simplifying이 무조건 간단한 편은 아니기 때문에)
| p | q | (p∧~q) | ~(p∨q) | (p∧~q)↔~(p∨q) |
| T | T | F | F | T |
| T | F | T | F | F |
| F | T | F | F | T |
| F | F | F | T | F |
3. 최종 output을 보면 tautology도 contradiction도 아님을 알 수 있다.

Solution : ~a∧(~f∨~d)
1. 주어진 statement를 simplifying하는 문제이다.
2. ~(a∨(f∧d)∨(a∧~b))
≡ ~a∧~(f∧d)∧(~a∨b) --- negation을 분배해주었다.
≡ ~a∧(~a∨b)∧~(f∧d) --- 흡수법칙을 쓰기 위해 자리를 바꿔주었다.
≡ ~a∧~(f∧d) --- 흡수법칙 ~a∧(~a∨b)=~a를 적용
≡ ~a∧(~f∨~d)
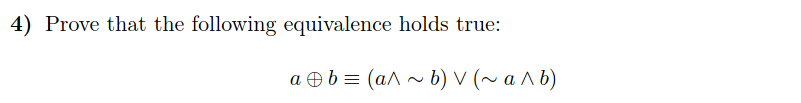
Solution : Equivalence가 성립한다.
1. 주어진 statement의 equivalence가 성립하는지 판단하는 문제이다.
2. aXORb
≡ (a∨b)∧~(a∧b) --- XOR의 개념 : aXORb=(a∨b)∧~(a∧b)
≡ (a∨b)∧(~a∨~b) --- negation을 분배해주었다.
≡ (a∧(~a∨~b))∨(b∧(~a∨~b)) --- 분배법칙
≡ (a∧~a)∨(a∧~b)∨(b∧~a)∨(b∧~b)
≡ (a∧~b)∨(b∧~a) --- (a∧~a)=c / (b∧~b)=c
따라서 우변과 동일하다.

Solution : Equivalence가 성립한다.
1. 주어진 statement의 equivalence가 성립하는지 판단하는 문제이다.
2. 접근방법을 모르겠어서 최고난이도 문제였음. 좌변과 우변을 보면 중앙에 있는 (b∧f)를 제외하고 같은 모양이다. 그래서인지 (b∧f)에 변형을 줘서 없애려고 하는 것 같다. 솔루션을 보니 (b∧f)에 tautology를 intersection하고 (b∧f)이 유지되도록 했다. 근데 이걸 생각해낼 수가 있냐구.
2. (a∧b)∨(b∧f)∨(~a∧f) ≡ (a∧b)∨(~a∧f)
좌변을 먼저 본다. 2에서 설명한 듯이...
≡ (a∧b)∨((a∨~a)∧(b∧f))∨(~a∧f) --- (a∨~a)=t를 넣어줌
≡ (a∧b)∨(a∧(b∧f))∨(~a∧(b∧f))∨(~a∧f) --- 분배법칙
≡ (a∧b)∨((a∧b)∧(b∧f))∨((~a∧b)∧(~a∧f))∨(~a∧f) --- 또 분배법칙
≡ (a∧b)∨(~a∧f) --- 흡수법칙
우변과 일치함을 알 수 있다.




