Recent Posts
Recent Comments
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
Tags
- ermodel
- GPT-1
- 써킷
- Tautology
- full adder
- CNF
- half adder
- 모두의네트워크정리
- Logical statement
- Decimal notation
- Contradiction
- Sentiment Analysis
- cnn
- 모순명제
- statement equivalence
- truth table
- 모두의네트워크
- 모두의네트워크요약
- dnf
- 명제
- relationaldatabaseschema
- Digital Logic Circuits
- 항진명제
- Gate
- 십진법
- 이진법 십진법 변환
- Circuit
- Binary notation
- 명제 동치
- 진리표
Archives
- Today
- Total
NLP Learner in Switzerland
[C] Basic Recursion ::: 재귀함수로 거듭제곱 나타내기 본문
728x90
반응형

까다로운 부분 알아가기
[1] 코드는 짧아보이지만 실제로 Recursion은 생각해내는게 간단하지 않다.
▶ 코딩초심자로서 일단 다른건 다 제쳐놓고 Recursion이면 무조건 if statement를 떠올리고,
▶ Stop condition(특정 조건일 때 이 Recursion이 멈춤)을 생각해서 이걸 제일 먼저 if에 코드화 해주고,
▶ 해당 Recursion함수내의 index 또는 차수의 감소/증가로 stop condition에 도달할 수 있게
이 두가지만 되더라도 일단 infinite loop의 늪에서 빠져나올 수 있는 것 같다.
[2] 거듭제곱을 어떻게 코드로 구현할까?
▶ 거듭제곱은 base(밑)^power(지수) 형태이다. 그리고 이를 expansion하면 base를 power번만큼 곱해준 것이다.

▶예시의 2^3=8를 보면, 2*2*2 = 8이 된다. Recursion이니까 일단 여기서 줄어드는게 뭔지만 찾아보면 뒤로 곱해질수록 power횟수가 감소하고 있다.
[3] Stop condition은
▶ power횟수가 줄어들다가 0이 되면 base의 숫자와 무관하게 공통적으로 base^(0)=1이 된다.
[4] 그리고 power횟수가 줄어들면서 곱해지는 부분을 구현한다.
#include <stdio.h>
int exponent(int x, int pow){
if(pow==0){ ----------------------- [3]
return 1;
}
return x*exponent(x,pow-1); ------- [4]
}
int main(){
int base,power;
printf("Please enter the base: ");
scanf("%d",&base);
printf("Please enter the power: ");
scanf("%d",&power);
printf("The result is: %d", exponent(base,power));
return 0;
}
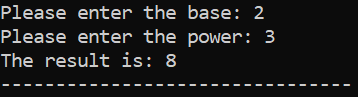
출력결과
'Algorithm in C > Exercise' 카테고리의 다른 글
| [C] Iteration and Recursion ::: 문자열에서 첫번째 대문자 찾아 인덱스를 반환하기 (0) | 2021.04.02 |
|---|---|
| [C] Multiple Recursion ::: 재귀호출이 2번 이상 일어나는 경우 (0) | 2021.04.01 |
| [C] Selection Sort in Ascending & Descending Order ::: 선택정렬 (0) | 2021.03.30 |
| [C] Matrix Multiplication ::: 행렬의 곱 (0) | 2021.03.29 |
| [C] Perfect Square Number ::: 제곱수 판별하기 (0) | 2021.03.29 |
Comments




